La Teoría General de la Relatividad

– Los postulados de la relatividad especial son dos. El primero explica que todo movimiento es relativo a cualquier otra cosa y el segundo afirma que la velocidad de la luz es siempre constante con respecto a cualquier observador.
– La teoría de la relatividad general se refiere al caso de movimientos que se producen con velocidad variable y tiene como postulado fundamental el principio de equivalencia, según el cual los efectos producidos por un campo gravitacional equivalen a los producidos por el movimiento acelerado.

Cuando Albert Einstein descubre los principios de la relatividad especial, se conocían dos fuerzas de la naturaleza, la electromagnética y la gravedad, y ambas tenían categorías distintas en dicha teoría. La relatividad especial surge para reconciliar el comportamiento de las ondas electromagnéticas con las propiedades mecánicas de los cuerpos en movimiento.

La teoría de Maxwell estaba de acuerdo con la relatividad especial (velocidad de la luz constante y maxima), a pesar de que se cambio la interpretación física anulándose el concepto del éter.. Por el contrario la teoría de la gravitación de Newton, resultaba incorrecta desde la perspectiva de la relatividad. Para Newton, la fuerza de la gravedad consiste en una acción instantánea a distancia, lo cual para Einstein carece de sentido dado que la simultaneidad de los acontecimientos no es posible cuando estos ocurren en dos lugares diferentes del espacio debido a que la información no viaja a velocidad infinita sino con un valor máximo pero finito igual al valor c = 300.000 km/seg.

Se denomina General por ser una generalización de la teoría especial. Recordemos que la teoría especial amplió el principio de relatividad desde la mecánica a toda la física, siempre que estuviéramos en sistemas de referencia inerciales, es decir en reposo o movimiento rectilíneo y uniforme. A través de la teoría general, Einstein va mas allá, diciendo que todos los sistemas de referencia son equivalentes, incluso aquellos que se mueven entre sí con movimientos acelerados.

¿Qué pasa cuando analizamos sistemas de referencia que se encuentran en movimiento acelerado?

Si vamos en un auto y este de repente cambia su velocidad, ya sea porque dobla o porque acelera (cambia la velocidad), nosotros en el interior del auto sentimos o que nos movemos para un costado ( el contrario al que dobla) o que nos pegamos contra el respaldo del asiento. Si frena nos pegamos contra el vidrio de adelante. En todos estos casos estamos experimentando una fuerza que denominamos inercial pero que no sabemos quien la provoca, es decir nada esta accionando contra nosotros para llevarnos a esa situación, simplemente hubo un cambio en las condiciones del movimiento.

De acuerdo a lo que ya sabemos respecto al movimiento relativo, podríamos decir que en todos estos casos, el auto es el sistema de referencia fijo y lo que en realidad se mueve hacia el costado o acelerando hacia delante o frenando es la tierra. Este razonamiento no nos parece lógico sino que el sentido común nos hace pensar que es el auto el que se esta moviendo y de allí los efectos inerciales, por eso es que Newton dijo que para el caso del movimiento acelerado, no existe el principio de relatividad sino que estos sistemas realmente tienen un estado de movimiento absoluto.

Entonces de acuerdo a este estado de la ciencia, cuando aparece Einstein teníamos dos conceptos:

El estado de movimiento uniforme es relativo.
El estado de movimiento acelerado es absoluto.
Einstein que siempre trataba de simplificar todo, pensaba que esto era raro y que la naturaleza debía ser más simple, es decir tener una sola verdad, que para el se podía expresar diciendo que cualquiera fuera el estado de movimiento de un cuerpo, siempre seria relativo. Esto es lo que durante mas de 10 años estuvo pensando para concluir en su teoría general de la relatividad.

¿Cuál era la intuición de Einstein para pensar la generalización de la teoría especial a la relatividad general?

Einstein decía que tanto las leyes de la mecánica newtoniana, como la teoría especial de la relatividad, son validas si las mismas se miden o se verifican dentro de sistemas especiales llamados galileanos, y no lo son en sistemas no galileanos. Einstein se pregunta ¿Qué hace que un tipo de sistemas de coordenadas sean preferibles respecto a otros. Redundantemente, por preferibles entendemos a aquellos donde se cumplen ciertas leyes de la naturaleza, las leyes de la mecánica y de la relatividad especial. Tengamos en cuenta que un sistema de referencia es una abstracción creada por el hombre. Esta paradoja o incongruencia Einstein la explica muy bien a partir de una comparación o imagen.

Dice así: supongamos que no conociéramos lo que es el fuego, y nos encontramos en una cocina donde hay dos ollas exactamente iguales con agua hasta la mitad, de una sale vapor y de la otra no. Nuestra lógica nos llevara a buscar la causa de esta diferencia aparentemente no razonable. Si viéramos que debajo de una de estas ollas hay una especie de luz azulada (una llama), aunque nunca hubiéramos tenido la experiencia del fuego, inmediatamente lo asociaríamos a la causa de la producción de vapor.

Si esto no ocurriera, estaríamos sorprendidos y perplejos e intentando encontrar la causa de este comportamiento extraño.

En forma análoga Einstein buscaba que era ese algo en la mecánica clásica o en la relatividad especial, al cual atribuir la diferente conducta de los cuerpos considerada respecto a los sistemas de referencia galileanos y no galileanos.

Newton vió esta objeción pero la invalidó sin una explicación lógica.

Mach la reconoció mas claramente y dijo que debía estudiarse la mecánica sobre una nueva base. Solo se podría mas tarde eliminar este estado d preferencia arbitrario por medio de una física que este conforme al principio de relatividad general. así las ecuaciones que expresan todas las leyes de la naturaleza no varían para ningún sistema de referencia, sin importar su condición de movimiento.

Volvamos nuevamente sobre los sistemas de referencia no inerciales. Imaginemos a un observador en un compartimiento en el espacio intergaláctico donde no se ejerce sobre el ningún tipo de fuerza. Imaginemos ahora que este compartimiento sufre una aceleración (es decir cambia su velocidad de reposo absoluto a una velocidad determinada v) siendo la misma constante a la que llamamos ¨a¨. En ese momento el observador suelta una moneda que tiene en su mano y vera que la misma cae hacia el piso del compartimiento con una aceleración constante igual a: -a.

Otro observador realiza el mismo experimento pero en un sistema de referencia inercial en presencia de un campo gravitatorio uniforme g, donde g=-a.

Al dejar caer la moneda este observador vera el mismo efecto que en el caso anterior, es decir a la moneda caer con una aceleración constante =-a.

¿Cómo podrían ambos observadores diferenciar si están en un sistema no inercial o en uno inercial dentro de un campo gravitatorio?

La respuesta es que no pueden, y es desde aquí que Einstein establece el postulado de la teoría general de la relatividad, diciendo que ningún experimento llevado a cabo localmente puede distinguir entre un sistema de referencia acelerado en forma constante y otro inercial (no-acelerado) pero en presencia de un campo gravitatorio.

Este postulado es un enunciado del principio de equivalencia entre la masa inercial y la masa gravitatorio. Así como la teoría especial de la relatividad nos lleva a fundir conceptos que se consideraban separados e independientes como son el espacio y el tiempo, en un nuevo concepto espacio-tiempo cuatridimensional; la teoría general requiere otro cambio en la visión de dicho espacio-tiempo, por el cual la causa de la gravedad esta dada por la deformación provocada en la geometría del espacio-tiempo en presencia de grandes masas. Es decir en lugar de tener un espacio-tiempo plano, este se curva en la vecindad de una masa. La curvatura se produce en el espacio cuatridimensional, por lo que es imposible que sea visualizada o percibida sensiblemente por seres como nosotros que somos tridimensionales. La teoría general de la relatividad trata entonces a la gravitación o gravedad como una curvatura del espacio-tiempo en cuatro dimensiones. Es decir como un fenómeno geométrico.

Si recordamos cuando hablamos de espacios curvos, veremos que la distancia mas corta entre dos puntos no es una recta sino una curva a la que llamamos geodesia.

En el espacio-tiempo la trayectoria de la tierra y los planetas alrededor del sol es una curva dado que esta es la distancia mas corta que puede recorrer a través de la geodesia del espacio. Esta geodesia surge por la curvatura que produce en el espacio- tiempo una masa como la del sol. Los efectos de la curvatura son mas apreciados cerca de grandes masas tales como las estrellas y los agujeros negros que se convierten en laboratorios importantes para la física de grandes energías.

Masa inercial y masa gravitatoria

Einstein analizaba que, tanto en la segunda ley de Newton F = m.a, como en la ley de gravitación universal F = G.m.M/R2, aparece una masa m.

Si ambas leyes son independientes entonces debería existir para cada cuerpo una masa inercial y una masa gravitatoria. Ahora bien todos los experimentos realizados para medir a ambas arrojaban los mismos resultados, es decir ambas masas eran iguales para el mismo cuerpo. Este resultado, ya conocido por Newton, hizo pensar a este que era totalmente casual. Por el contrario, Einstein dijo que el concepto de aceleración que surge de la 2a ley de Newton, debía estar relacionado con el concepto de gravedad.

Si dos objetos tienen diferente peso, por ejemplo una bala que pesa 100 veces mas que una bolita, significa que la gravedad ejerce sobre la bala una fuerza 100 veces mayor que sobre la bolita, sin embargo ignorando la resistencia del aire sabemos y demostramos experimentalmente que si las arrojamos desde una misma altura, ambas caen en el mismo tiempo al piso. Esto a lo mejor no lo pensamos detenidamente, pero es totalmente extraño y contra el sentido común. ¿Por qué ocurre así?, Newton dijo que al mismo tiempo que la gravedad arrastra hacia abajo a los cuerpos, estos se resisten a moverse, ese es el concepto de inercia, es decir resistencia al cambio de movimiento. Si esta detenido: resistencia a moverse, si se mueve y se lo acelera: resistencia a aumentar la velocidad, si se lo quiere detener: resistencia a parar. Es decir la inercia nos da una idea de vagancia física propia de los cuerpos de cualquier tipo.

Entonces la bala si bien tiene 100 veces mas fuerza de arrastre por la gravedad de la tierra (asumimos que hacemos el experimento en la tierra), también tiene como contrapartida 100 veces más resistencia a moverse.

Si esto no fuera así, objetos de diferentes pesos caerían en diferentes tiempos desde la misma altura.

Decíamos que para Newton decir que la masa gravitacional fuera igual a la masa inercial era una casualidad, el no sabia cual era la razón de esta igualdad.

Einstein por el contrario estableció un postulado, que se conoce como principio de equivalencia, diciendo que la masa inercial y la masa gravitacional son la misma cosa.

Para ejemplificar esto un poco mas, Einstein pensaba en una persona encerrada en una caja tipo ascensor, en el espacio, y decía que si a esa caja se la ataba a aun cohete que la aceleraba a un valor determinado (el valor de g = 9.80 m/seg2), la persona en su interior no podría distinguir entre esta situación (aceleración arrastrada por un cohete) o pensar que la caja estaba depositada en la superficie de la tierra, y el parado sobre la misma.

De allí mostró la imposibilidad de diferenciar entre una fuerza gravitacional y una inercial producida por una aceleración. A partir de este razonamiento, podemos considerar que los sistemas de referencia que se encuentran en un estado de movimiento acelerado entre ellos, es indistinto hablar de efectos inerciales como de efectos gravitatorios.

La teoría general de la relatividad extiende entonces el postulado de la relatividad especial a sistemas de referencia que estén en estado de movimiento acelerado.

Todas las leyes de la naturaleza son las mismas con respecto a cualquier observador, sea cual fuere su estado de movimiento relativo a otro sistema: reposo, movimiento uniforme o acelerado.

Observador Inercial

Un observador inercial es un sistema que recolecta información en un sistema de coordenadas espacio-tiempo, en el cual se identifican como coordenadas espaciales a x,y,z y como coordenada temporal a t. Un punto en dicho espacio-tiempo es un evento.

Para que dicho sistema sea llamado inercial se deben cumplir las siguientes 3 condiciones

La distancia entre dos puntos espaciales P1(x1,y1,z1) y P2(x2,y2,z2) es independiente del tiempo t.
Los relojes que miden el paso del tiempo en cada punto del espacio-tiempo están sincronizados y funcionan a la misma velocidad, es decir cada tic es simultaneo.
La geometría de dicho espacio para un tiempo t constante es euclidiana.
Una observación de un observador inercial significa asignar a un evento las coordenadas x, y , z de la localización de su ocurrencia (donde ocurrió) y el tiempo t leído en el reloj que esta ubicado en el lugar del evento, es decir en P = x, y, z.

Debemos aclarar que NO ES el tiempo que marca el reloj de la muñeca del observador ubicado en el origen O (0,0,0) cuando observa el evento en P (x,y,z).

Esto es así porque según sabemos, la ocurrencia del evento y la observación del mismo por parte del observador en O, no son eventos simultáneos dado que la luz, que es el mecanismo de transmisión de la información desde P hasta O, tiene una velocidad finita.

Gráfico de Minkowski (Diagrama espacio-tiempo)

Este tipo de diagramas permite un enfoque geométrico de la teoría especial de la relatividad. Graficamos un par de ejes coordenados donde las abscisas sean una dimensión espacial x, y las ordenadas una dimensión temporal pero algo diferente. Ponemos en ella el valor c.t, donde c es una constante conocida (la velocidad de la luz) y t es el tiempo variable. De esta manera lo que representamos en este eje, será la distancia que recorre la luz en el tiempo t. De esta manera tenemos un grafico de las mismas dimensiones (dimensiones de espacio, Ej. Metros). Al ser c una constante, adoptamos para ella un valor que sea más accesible para trabajar, dándole así el valor c=1.

Una línea en este grafico se la denomina línea del mundo del objeto que estamos observando, y representa por un lado (eje de abscisas), la posición de dicho objeto en el espacio que llamamos para una sola dimensión espacial variable x. Por otro lado, en el eje de las ordenadas, el momento en que dicho objeto ocupo dicha posición x en el espacio. En lugar de decir que ese tiempo es a los N segundos o minutos u horas, diremos que el mismo es la distancia que recorrió la luz a su velocidad constante c en el tiempo t=N.

La pendiente de una línea del mundo de un objeto nunca puede ser menor que 1, es decir el ángulo mínimo que forma la línea del mundo con el eje de las abscisas será de 450. Esto resulta así por ser c la velocidad máxima a alcanzar por cualquier objeto. Si el objeto se moviera a la velocidad máxima de la luz partiendo desde el origen del sistema, el punto alcanzado será tal que la medida de la ordenada de dicho punto será c.t la distancia recorrida por la luz, cuyo valor es igual a la medida de la x, por que este es el espacio recorrido por un objeto durante un tiempo t a la velocidad c (espacio = velocidad x tiempo). Es decir ambos valores serán iguales, y por un simple razonamiento trigonométrico sobre el triangulo que se dibuja en los ejes, resultara que la tangente del ángulo será igual a 1, por lo que el ángulo será de 450. No puede ser menor dado que esto implicaría que el objeto recorriera una distancia superior a la que puede recorrer la luz, lo cual es imposible según el 20 postulado de la teoría especial de la relatividad.

Habiendo deducido el porque del ángulo mínimo en las líneas del mundo del grafico de Minkowski, detengámonos un poco mas en el.

Decíamos que a un punto en el grafico de Minkowski se lo denomina evento. Cualquier evento que ocurre en el mundo físico, ocurre en una determinada ubicación en el espacio y en un determinado instante o momento del tiempo.

Antes del advenimiento de la teoría especial de la relatividad, solo se consideraba al espacio tridimensional y al tiempo como algo separado porque este parecía un continuo en si mismo, independiente y absoluto; es decir el tiempo pasa igual para todos. A partir de los desarrollos de Einstein, se supo y comprobó que el tiempo no es absoluto sino que depende del estado de movimiento de los sistemas de referencia donde se lo mida tal como surge de las transformadas de Lorentz. Habíamos deducido que eventos simultáneos para un observador que ocurren en lugares distintos, no se presentan como simultáneos a otro observador que se encuentra en un sistema de referencia en movimiento respecto al primero.

En un espacio euclidiano de 3 dimensiones, sabemos que la distancia entre dos puntos por ejemplo un punto P (x,y,z) y el origen (0,0,0) se calcula con la ecuación : d2=x2+y2+z2

Sabemos también que esta distancia no varia cuando se la mida en otro sistema que este en movimiento respecto al primero, es decir d2=x'2+y'2+z'2.

Vimos que en el espacio cuatri-dimensional de Minkowski hacíamos un reemplazo de la variable tiempo t por una constante multiplicada por t. Esa constante es i.c, donde i es la raíz cuadrada de –1, y c la velocidad de la luz (¿por qué hacemos esto? No se). Es decir este es un numero imaginario puro cuyo modulo es la distancia recorrida por la luz en el tiempo t, que es lo que antes en dos dimensiones habíamos explicado. Este cambio en la forma de medir el tiempo apunta a poder medir la variable tiempo con las mismas dimensiones que la variable espacio. Vimos antes y se explicita formalmente en las transformadas de Lorentz que ambos, tiempo y espacio, son parte de una misma entidad llamada espacio-tiempo. De allí la necesidad de tener las mismas dimensiones.

Si definimos que el espacio-tiempo localmente, tiene propiedades de espacio euclidiano, entonces la formula de la distancia según vimos en tres dimensiones vale también para cuatro:

d2= x2+y2+z2+(i.c.t)2, o sea que

d2= x2+y2+z2 –c2.t2

Construcción de un grafico de Minkowski (ejes no ortogonales)

Habíamos dicho que dado que c es una constante nada impide que le demos a la misma el valor 1.
En el grafico bidimensional de Minkowski tenemos que la pendiente de una línea del mundo que esta dada por la formula ?t/?x es la inversa de la velocidad.
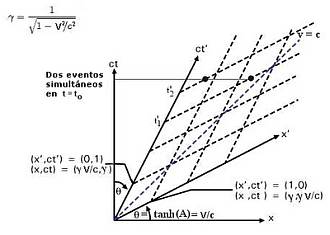
Cada observador es un sistema de coordenadas espacio-tiempo. Dado que todos los observadores miran a los mismos eventos (el mismo espacio-tiempo) es posible dibujar los ejes coordenados de un observador en el diagrama espacio-tiempo del otro. Para esto debemos utilizar los postulados de la teoría especial de la relatividad. Vemos el procedimiento.

La pregunta entonces es ¿Como dibujamos dos sistemas que se mueven uno respecto a otro a la velocidad v, y en donde en ambos se da el 2o principio de Einstein, c= constante?

Dibujamos un para de ejes coordenados perpendiculares. Este será para nosotros el sistema en reposo S (x, t).
Si el sistema S' (x',t') que tiene el mismo origen O'=O, se mueve con velocidad v respecto de S; sabemos que el eje t' formara con el eje t un ángulo a tal que Sen a = ?t/?x = 1/v

Así como en un espacio euclidiano de tres dimensiones la separación entre dos puntos se denomina distancia la cual es invariante y se calcula con la formula d2=x2+y2+z2, en el espacio-tiempo se denomina intervalo a lo mismo, salvo que ahora dado que la dimensión tiempo esta dada por i.c.t, su cuadrado será -c2t2, y como adoptamos para c un valor 1, dicho termino será –t2.

El teorema de invarianza del intervalo dice que la el intervalo permanece constante en los diferentes sistemas de referencia, por lo tanto dados dos eventos E y P su intervalo será tal que (?x)2+(?y)2+(?z)2-(?t)2=0

El intervalo de los mismos eventos en el espacio-tiempo S' será invariante siendo entonces que (?x')2+(?y')2+(?z')2-(?t')2=0 .
A partir de esto definimos como intervalo entre cualquier de dos eventos, los cuales no necesariamente estarán en la misma línea del mundo del mismo haz de luz al valor ?s tal que (?s)2=(?x)2 +(?y)2+(?z)2-(?t)2
Si (?s)2=0 para dos eventos en el sistema K (t,x,y,z), entonces por el teorema de la invarianza de los intervalos, (?s')2=0 para los mismos eventos usando sus coordenadas en el sistema K' (t',x',y',z').

Se demuestra que (?s)2=(?s')2. Es decir el intervalo entre dos eventos es el mismo cuando es calculado por un observador inercial.

Si (?s)2>0, significa que (?x)2+(?y)2 +(?z)2 >(?t)2 en cuyo caso al ser los incrementos espaciales superiores al incremento temporal, se dice que los eventos están separados espacialmente. Por el contrario si ocurre lo contrario ( ?s)2 <0, los eventos se dice que están separados temporalmente. Si (?s)2 =0 los eventos están sobre los mismos rayos de luz, y su separación es nula

Aquellos eventos que están sobre los mismos rayos de luz tendrán separación nula con otro evento determinado llamado A y en un grafico tridimensional espacio-tiempo (dos dimensiones espaciales y una temporal) se ubicaran sobre un doble cono invertido cuyo vértice es el evento A. A este doble cono se lo llama cono de luz del evento A y muestra las posiciones posibles de eventos ocurridos en el pasado y en el futuro del evento A.

Fuente: pardell.es