Claude Shannon y la información
El que veamos la TV y nos comuniquemos por móvil parece hoy algo trivial, pero no ha sido así siempre. Ha tenido que haber mentes fuera de lo común para que haya sido posible. Y hoy quiero hablaros de una de esas mentes que hicieron posible que la era de la información sea una realidad.
Las primera imágenes por satélite recibidas en la historia fueron gracias al Telstar, lanzado allá por el año 1962. Enviar las imágenes desde la Tierra hasta el satélite no representaba un gran problema. Se hacía con una antena parabólica dirigida hacia al mismo con una potencia de muchísimos kilovatios. Lo difícil era que las imágenes volvieran a bajar a la Tierra, ya que el satélite obtenía su energía por unas células solares muy pequeñas. Apenas podía generar unas pocas decenas de vatios de potencia de radio: más o menos, las mismas que el faro de un automóvil. Además, el satélite era tan pequeño que no podía llevar una antena suficientemente grande, con lo que las ondas que devolvía se expandían en una zona amplísima de superficie, llamada huella satelital. La del Telstar tenía aproximadamente un millón de kilómetros cuadrados.
La equivalencia en un ejemplo cotidiano sería como poder ver la luz de unas 10 velas a 40.000 kilómetros de distancia. Como esa potencia se emitía sobre una superficie de un millón de kilómetros cuadrados, la huella tenía una diezmillonésima de millonésima de vatio. Una verdadera miseria.
En el fondo, lo que hacen las señales es poner los electrones de los receptores en movimiento. Hay que pensar que los receptores utilizan, por otro lado, corriente eléctrica, y recordemos que también tienen electrones en movimiento por sus componentes: están corriendo alrededor de los núcleos de los átomos y no paran de moverse. Y si ese movimiento, llamado ruido de señal, es comparable a la potencia de las ondas que hemos recibido estamos listos, pues una vez recibida la señal se tenía que amplificar lo que significaba que también se amplificaba el ruido. Un problema realmente serio, ¿verdad? ¿Se os ocurre cómo resolverlo? Pues a ese problema se enfrentaron los ingenieros de aquella época, y lo hicieron de dos maneras.
La primera fue utilizando la fuerza bruta: una enorme antena llamada Arthur recibiría la señal. Pero como aun así el ruido era considerable, decidieron optar por la segunda forma: enfriar todos los cables y elementos eléctricos para que los electrones se movieran más despacio y generasen menos ruido: nada menos que en helio líquido a -269 ºC.
Y hoy día, nuestros miserables móviles son capaces de captar sin problemas la señal de un satélite y, ¿verdad que no utilizan helio líquido? Somos incluso capaces de detectar la señal de los pequeños vehículos espaciales que caminan por Marte sin necesitar poner nuestros receptores en helio líquido. ¿Qué ha cambiado? ¿Cómo lo hacemos? Quien sentó las bases para poder conseguirlo fue un excepcional hombre llamado Claude Shannon.
Nacido en Michigan (EEUU), en 1916 (30 de abril), su héroe de pequeño era Thomas Alva Edison, de quien era un primo lejano. Tras obtener los títulos en Matemáticas e Ingeniería Electrónica en la universidad de Michigan, ingresó en el MIT para continuar en sus estudios. Mientras estudiaba, trabajó como asistente para controlar el Analizador Diferencial de Vannevar Bush, la máquina calculadora más avanzada de la época, constituida por un sistema mecánico dirigido por un circuito de relés, y utilizada para resolver ecuaciones diferenciales.
Su primera publicación, en 1938, fue su propia tesis en Ingeniería. Proponía, por un lado, la discretización de todo circuito elemental en dos estados, cerrado y abierto, y su representación mediante sendos valores (0 y 1) que se hacen corresponder respectivamente con la falsedad o verdad de una proposición lógica. Sugería, por otro, el empleo del álgebra de Boole para el análisis de circuitos más complejos.
Dicha álgebra consta de dos valores: 0 y 1; y se puede utilizar de modo que 1 signifique "ON" cuando el interruptor este cerrado y el circuito encendido, y 0 significa "OFF" cuando el interruptor este abierto y el circuito apagado. La unidad que utilizó fue el binary digit, más conocida como bit. Seguro que os suena.
J.B.S. Haldane calculó el número de bits transmitidos por una abeja obrera a sus compañeras de la colmena cuando "danza" la ubicación de una fuente de alimento (alrededor de 3 bits para la información de la dirección y otros tres para la distancia).
Sus resultados tuvieron un gran impacto y por ellos recibió el premio más importante que concedían las sociedades de ingeniería de Estados Unidos a menores de treinta años, el Alfred Noble (no confundir con el Premio Nobel).
En 1940 obtuvo el doctorado en Matemáticas, pasando a trabajar durante un año en el Instituto de Estudios Avanzados de Princeton. Transcurrido dicho año entró a trabajar en la Bell Telephone en New Jersey, realizando investigaciones para obtener mejoras en la transmisión de información a través de las líneas telefónicas a larga distancia. Fue en la Bell donde trabajo con lumbreras como Harry Nyquist (especialista en señales), John Pierce (experto en comunicaciones por satélite) John Bardeen (el de los dos tercios de Nobel), Walter Houser Brattain y William Bradford Shockley (estos dos últimos, también premios Nobel) y George Stibitz (quien había construido, ya en 1938, un ordenador con relés).
Una de las intuiciones de Shannon consistió en ver que se podía intercambiar tiempo por potencia. Es decir, la potencia necesaria para transmitir y recibir con éxito una señal en un ambiente dominado por el ruido podía cambiarse por el tiempo empleado en hacer esa transmisión. Por ejemplo, imaginemos que estamos en una de las aceras de una gran avenida, con un montón de vehículos circulando. Queremos transmitir un mensaje a otra persona en la otra acera: "Ya nos veremos después". Lo gritamos, pero nuestro amigo apenas consigue oírnos. Ha captado el "nos", pero el resto no. En un determinado instante, no hay tanto tráfico y aprovechamos para repetir gritando. Nuestro amigo capta "veremos" y "después". En una tercera vez no consigue captar nada y a la cuarta vez, capta el "ya". Nuestro amigo es capaz de reconstruir la frase completa y sin errores, sí, pero ha sido necesario repetir el mensaje cuatro veces. Si el ruido de tráfico hubiera sido mayor, hubiéramos tenido que repetir la frase más veces; y con menos tráfico, menos veces. La repetición del mensaje es un ejemplo de "codificación" del mismo.
Por supuesto, hay mejores formas de transmitir mensajes con ruido, podemos codificarlos mensajes mucho mejor, sustituyendo el mensaje original por símbolos matemáticos. Un mensaje codificado es más largo que el original y, por tanto, se requiere más tiempo para su envío; pero una vez codificado, soporta mucho mejor el ruido de fondo generado dentro del receptor de radio, así que vale la pena gastar más tiempo en enviarlo.
Shannon explicó todo esto con rigor matemático. Junto a otro ingeniero llamado Ralph Hartley establecieron el Teorema de Shannon-Hartley, que dice, más o menos, que la tasa máxima a la que se puede transmitir un mensaje está limitada por la intensidad de señal en relación con el ruido de fondo.
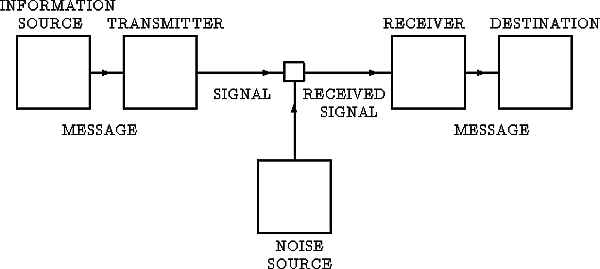
Introdujo la definición técnica de "información" en 1948. Como empleado de la Bell, estaba interesado en medir la información como bien económico. Enviar mensajes por una línea telefónica es costoso y mucho de lo que se transmite en el mensaje no es información, sino redundancia. Se podría ahorrar dinero recodificando el mensaje de tal modo que no hubiera redundancia. Por ejemplo, si decimos "Rover es un perro caniche", estamos dando información de más, ya que al decir caniche, ya sabemos que es un perro. Este término, redundancia, fue el segundo introducido por Shannon. Pero quería llegar más allá: buscaba una forma matemática de capturar la idea de que cualquier mensaje podía ser dividido en información (por lo que vale la pena pagar), redundancia (lo que podría eliminarse del mensaje que incurre en un gasto extra) y ruido (basura aleatoria).
Estimemos, sugirió Shannon, tomemos la ignorancia o incertidumbre del receptor antes de recibir el mensaje y comparémosla luego con la ignorancia remanente después de que ese receptor haya recibido el mensaje. La cantidad de reducción de la ignorancia es la cantidad de información. Al hacer el desarrollo matemático, la fórmula que le salió era idéntica a la de la entropía que años antes nos había enseñado el genial teórico Ludwig Boltzmann.
Con sus propias palabras:
Pensé en llamarlo información, pero era una palabra demasiado utilizada, así que decidí denominarla incertidumbre. Cuando lo discutí con John von Neumann, él tuvo una idea mejor: Deberías llamarle entropía, por dos razones: primero porque tu función de incertidumbre ha sido utilizada en mecánica estadística con ese nombre, así que ya tiene un nombre; y en segundo lugar, y esto es más importante, porque nadie sabe lo que es la entropía realmente, de modo que en una discusión siempre tendrás ventaja.
Shannon estaba muy interesado en la idea de que las máquinas pudieran aprender, y por ello en 1952 inventó un ratón eléctrico, llamado Teseo, capaz de encontrar el camino correcto en un laberinto. También fue uno de los primeros que trabajó en un programa contra el que se pudiera jugar una partida de ajedrez. Preguntado en una ocasión por un periodista si las máquinas podían pensar replicó: ¡Naturalmente! ¡Usted y yo somos máquinas y vaya si pensamos!. Así que podemos considerarlo como uno de los padres de la inteligencia artificial.
También demostró que si los mensajes que se enviaban se hacían con una codificación de autocorrección, la señal se podía transmitir, por ejemplo, el bit de paridad; pero también sugirió la idea contraria. Si se quería encriptar un mensaje podía hacerse que llevara ruido con una clave mezclándolo al mensaje original. Y esta ha sido la base de muchos sistemas criptográficos. El propio Shannon desarrolló este tipo de aplicaciones y fue nombrado por ello consultor en materia de criptografía del gobierno de Estados Unidos, siendo precisamente su sistema el que emplearon Churchill y Roosevelt para mantener conferencias transoceánicas durante la Segunda Guerra Mundial. Todos sabemos que si de criptografía se habla, el nombre que más destaca es Alan Turing. Pues bien, se conocieron y mantuvieron contacto durante dos meses. ¿Os imagináis una conversación entre ellos dos?
Era famoso en los laboratorios Bell por montar en monociclo realizando equilibrios por los pasillos. Tenía un imaginativo sentido del humor. Cierta vez construyó una caja con un único interruptor en su exterior basado en una idea de Marvin Minsky. Si uno tiraba de la palanca, la tapa de la caja se abría lentamente, aparecía una mano mecánica, descendía hasta el interruptor y cerraba la caja. Luego, la mano se retiraba otra vez dentro de la caja y la tapa se cerraba. Hay quien ha hecho una máquina así… ¡con LEGO!
Arthur C. Clarke comentó sobre este artilugio: Hay algo de inefablemente siniestro en una máquina que no hace nada, absolutamente nada, excepto apagarse a sí misma.
Shannon se jubiló a los cincuenta años, un poco para huir de la pesada tarea de divulgar sus pensamientos y, sobre todo, para poder dedicarse a sus ingenios. Y si a esto añadimos que la mayoría de sus trabajos han estado clasificados como secretos durante largo tiempo, ya podemos entender por qué es poco conocido por el gran público, incluido muchos especialistas.
En una de sus últimas entrevistas dijo:
Siempre he perseguido mis intereses sin prestar mucha atención a su valor financiero o para el mundo; he dedicado muchas horas a cosas totalmente inútiles.
Murió tras varios años de lucha con el Alzheimer el 24 de febrero de 2001.
En el obituario, su esposa Elizabeth Moore, con quien se había casado en 1949 y había tenido 3 hijos, dijo que de no haber sido por su enfermedad, se hubiera quedado perplejo por la revolución digital. Pues no sé si realmente hubiera sido así, pero sí puedo asegurar que cualquier persona con formación científica o técnica queda mucho más perpleja al intentar entender cómo todas estas cosas se le pudieron ocurrir a un solo hombre.
Fuentes:
Richard Dawkins, El capellán del diablo.
Graham Tattersall, Cómo los números pueden cambiar tu vida.
en.wikipedia.org/wiki/Claude_Shannon
dma.eui.upm.es/historia_informatica/Doc/Personajes/ClaudeShannon.htm
fortunecity.es/imaginapoder/artes/368/escuela/shannon/shannon.htm
claudeelwoodshannon.blogspot.com
Encuentre más del mismo autor en historiasdelaciencia.com. Artículo amparado con Licencia Creative Commons reconocimiento 2.5.
Fuente: omalaled – historiasdelaciencia.com